আয়তক্ষেত্র কাকে বলে
যে চতুর্ভুজ এর বিপরীতে থাকা বাহুগুলো পরস্পর সমান ও সমান্তরাল হয় এবং কোনগুলি সমকোণ হয় তাকে আয়তক্ষেত্র বলা হয়।
অন্যভাবে বলা যায়, যে চতুর্ভুজ এর বিপরীত বাহুগুলো পরস্পর সমান হয় এবং প্রতিটি কোণ সমকোণ হয় তাকে আয়তক্ষেত্র বলে।
আয়তক্ষেত্রের সংক্ষিপ্ত সংজ্ঞা হল- যে চতুর্ভুজ এর সবগুলি কোণ সমকোণ হয় তাকে আয়তক্ষেত্র বলা হয়। এছাড়াও বলা যায় আয়ত দ্বারা আবদ্ধ ক্ষেত্রকে বলা হয় আয়তক্ষেত্র।
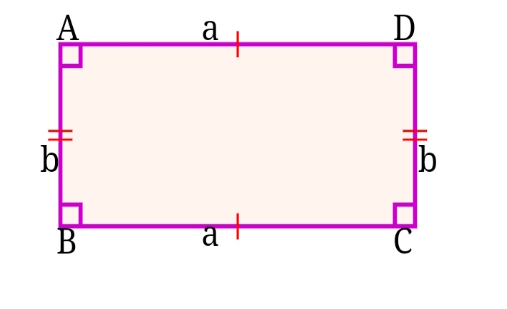
চিত্রে, ABCD একটি চতুর্ভুজ। AD ও BC পরস্পর বিপরীত বাহু ও তাদের দৈর্ঘ্য পরস্পর সমান এবং AD ও BC পরস্পর সমান্তরাল। অর্থাৎ, AD∥BC এবং AD = BC. আবার, AB ও CD পরস্পর বিপরীত বাহু ও তাদের দৈর্ঘ্য পরস্পর সমান এবং AB ও CD পরস্পর সমান্তরাল। অর্থাৎ, AB∥CD এবং AB = CD.
তাছাড়া, ABCD চতুর্ভুজের কোণগুলো সমকোণ বা ৯০°। অর্থাৎ,
∠ABC = এক সমকোণ বা ৯০°,
∠BCD = এক সমকোণ বা ৯০°,
∠ADC = এক সমকোণ বা ৯০° এবং
∠BAC = এক সমকোণ বা ৯০°।
এখানে দেখা যাচ্ছে যে, ABCD চতুর্ভুজটি আয়তক্ষেত্রের সব বৈশিষ্ট্য ধারণ করেছে। সুতরাং বলা যায়, ABCD একটি আয়তক্ষেত্র।
আয়তক্ষেত্রের পরিসীমা
আয়তক্ষেত্রের বাহুগুলির সমষ্টিকে আয়তক্ষেত্রের পরিসীমা বলা হয়। অতএব আয়তক্ষেত্রে চারটি বাহুর দৈর্ঘ্য যোগ করলে পাওয়া যাবে আয়তক্ষেত্রের পরিসীমা।
আয়তক্ষেত্রের পরিসীমা নির্ণয়ের সূত্র
আয়তক্ষেত্রের বিপরীত বাহুদ্বয় পরস্পর সমান। মনেকরি ABCD আয়তক্ষেত্রের দৈর্ঘ্য AB = CD = a এবং প্রস্থ BC = AD = b.
সুতরাং আয়তক্ষেত্রের পরিসীমার সূত্রটি হবে,
আয়তক্ষেত্রের পরিসীমা = (AB + BC + CD + AD) একক
বা, আয়তক্ষেত্রের পরিসীমা = (a + a+ b + b) একক
বা, আয়তক্ষেত্রের পরিসীমা = (2a + 2b) একক
∴ আয়তক্ষেত্রের পরিসীমা = 2×(a + b) একক
সুতরাং, আয়তক্ষেত্রের পরিসীমা =২×( দৈর্ঘ্য + প্রস্থ ) একক
আয়তক্ষেত্রের দৈর্ঘ্য a এবং প্রস্থ b হলে,
আয়তক্ষেত্রের পরিসীমা = 2×(a + b) একক।
আয়তক্ষেত্রের পরিসীমা =২×( দৈর্ঘ্য + প্রস্থ ) একক।
উদাহরণঃ
একটি আয়তক্ষেত্রের দৈর্ঘ্য ৬ সেমি ও প্রস্থ ৫ সেমি হলে আয়তক্ষেত্রের পরিসীমা কত হবে?
সমাধানঃ মনে করি, আয়তক্ষেত্রটির দৈর্ঘ্য a = ৬ সেমি এবং প্রস্থ b = ৫ সেমি।
আয়তক্ষেত্রের পরিসীমা = ২ ×(দৈর্ঘ্য + প্রস্থ) একক
বা, আয়তক্ষেত্রের পরিসীমা = ২ ×(a + b) একক
বা, আয়তক্ষেত্রের পরিসীমা = ২ ×(৫ + ৪) সেমি
বা, আয়তক্ষেত্রের পরিসীমা = (২ ×৯) সেমি
∴ আয়তক্ষেত্রের পরিসীমা = ১৮ সেমি।
আয়তক্ষেত্রের ক্ষেত্রফল
আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থের গুণফলকে আয়তক্ষেত্রের ক্ষেত্রফল বলে।
আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র
মনে করি, আয়তক্ষেত্রের দৈর্ঘ্য a একক, প্রস্থ b একক এবং ক্ষেত্রফল A বর্গ একক।
সুতরাং, আয়তক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × প্রস্থ) বর্গ একক
∴ আয়তক্ষেত্রের ক্ষেত্রফল, A = ab বর্গ একক
আয়তক্ষেত্রের দৈর্ঘ্য a, প্রস্থ b এবং ক্ষেত্রফল A হলে,
আয়তক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × প্রস্থ) বর্গ একক
আয়তক্ষেত্রের ক্ষেত্রফল, A = ab বর্গ একক
উদাহরণঃ
একটি আয়তক্ষেত্রের দৈর্ঘ্য ৪ সেমি ও প্রস্থ ৩ সেমি হলে আয়তক্ষেত্রটির ক্ষেত্রফল কত?
সমাধানঃ মনে করি, আয়তক্ষেত্রটির দৈর্ঘ্য a = ৪ সেমি ও প্রস্থ b = ৩ সেমি।
আয়তক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক
বা, আয়তক্ষেত্রের ক্ষেত্রফল = (a × b) বর্গ একক
বা, আয়তক্ষেত্রের ক্ষেত্রফল = (৪ × ৩) বর্গ সেমি
বা, আয়তক্ষেত্রের ক্ষেত্রফল = ১২ বর্গ সেমি
∴ আয়তক্ষেত্রের ক্ষেত্রফল = ১২ বর্গ সেমি।
আয়তক্ষেত্রের কর্ণ
ক্ষেত্রে বিপরীত দুটি শীর্ষবিন্দু যোগ করে যে রেখাংশ সৃষ্ট হয় তাকে আয়তক্ষেত্রের কর্ণ বলা হয়। আয়তক্ষেত্রের দুই জোড়া বিপরীতে থাকা শীর্ষবিন্দু সংযুক্ত করলে দুইটি কর্ণ পাওয়া যাবে। আয়তক্ষেত্রের দুটি কর্ণের দৈর্ঘ্য পরস্পর সমান হবে এবং কর্ণ দুইটি পরস্পরকে সমদ্বিখন্ডিত করবে।
আয়তক্ষেত্রের কর্ণের সূত্র
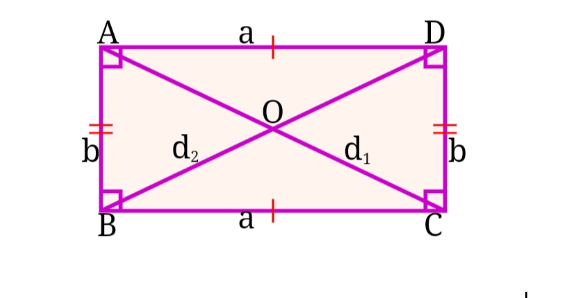
দুই কর্ণ বিশিষ্ট আয়তক্ষেত্র চিত্র
মনেকরি, ABCD একটি আয়তক্ষেত্র যার দৈর্ঘ্য AD = BC = a এবং প্রস্থ AB = CD = b. আয়তক্ষেত্রটির একটি কর্ণ AC = d1 এবং অপর কর্ণ BD = d2.
তাহলে, সমকোণী ত্রিভুজ △ABC -এ
∠ABC = ৯০° এবং যার অতিভুজ d1.
পিথাগোরাসের উপপাদ্য অনুসারে,
AC2 = BC2 + AB2
বা, d12 = a2 + b2
∴ d1 = √(a2 + b2)
∴ কর্ণ = √(দৈর্ঘ্য)2 + (প্রস্থ)2 একক
আয়তক্ষেত্রের দৈর্ঘ্য a একক, প্রস্থ b একক এবং কর্ণ d একক হলে,
কর্ণ = √(দৈর্ঘ্য)2 + (প্রস্থ)2 একক
d = √(a2 + b2) একক
উদাহরণঃ
একটি আয়তক্ষেত্রের দৈর্ঘ্য ৩৫ সেমি ও প্রস্থ ১২ সেমি হলে আয়তক্ষেত্রের কর্ণ কত?
সমাধানঃ মনে করি, আয়তক্ষেত্রটির দৈর্ঘ্য a = ৩৫ সেমি এবং প্রস্থ b = ১২ সেমি।
এখন আয়তক্ষেত্রের কর্ণ নির্ণয়ের সূত্র ব্যবহার করে পাওয়া যায়,
আয়তক্ষেত্রের কর্ণ = √(দৈর্ঘ্য)2 + (প্রস্থ)2 একক
বা, আয়তক্ষেত্রের কর্ণ = √a2 + b2 একক
বা, আয়তক্ষেত্রের কর্ণ = √(৩৫)২ + (১২)২ সেমি
বা, আয়তক্ষেত্রের কর্ণ = √১২২৫ + ১৪৪ সেমি
বা, আয়তক্ষেত্রের কর্ণ = √১৩৬৯ সেমি
বা, আয়তক্ষেত্রের কর্ণ = √(৩৭)২ সেমি
বা, আয়তক্ষেত্রের কর্ণ = ৩৭ সেমি
∴ আয়তক্ষেত্রের কর্ণ = ৩৭ সেমি
আয়তক্ষেত্রের বৈশিষ্ট্য
- আয়তক্ষেত্রের কর্ণদ্বয় পরস্পর সমান হয়ে থাকে।
- এর কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
- আয়তক্ষেত্রের দৈর্ঘ্য এবং প্রস্থের যোগফলের দ্বিগুণ হবে এর পরিধি।
- আয়তক্ষেত্রের বিপরীতে থাকা বাহুগুলি পরস্পর সমান হবে।
- আয়তক্ষেত্রের কর্ণ দুটোর দৈর্ঘ্য সমান হবে।
- আয়তক্ষেত্রের চারটি শীর্ষবিন্দু এবং চারটি বাহু রয়েছে।
- প্রতিটি আয়তক্ষেত্রই একটি চতুর্ভুজ।
- আয়তক্ষেত্র একটি অনিয়মিত বহুভুজ।
- এর প্রতিটি কোণ ৯০ ডিগ্রী বা সমকোণ।
- প্রতিটি শীর্ষে নব্বই ডিগ্রীর সমান কোণ রয়েছে।
- সকল অভ্যন্তরীণ কোণের সমষ্টি ৩৬০ ডিগ্রি সমান।
উপসংহার
পরিশেষে বলা যায় যে, যে চতুর্ভুজ এর সবগুলি কোণ সমকোণ হয় আয়তক্ষেত্র। এছাড়াও বলা যায় আয়ত দ্বারা আবদ্ধ ক্ষেত্রকে বলা হয় আয়তক্ষেত্র। আজ এই আর্টিকেলের মাধ্যমে আমরা জানলাম আয়তক্ষেত্র কাকে বলে, আয়তক্ষেত্রের বৈশিষ্ট্য, ক্ষেত্রফল ও পরিসীমার সূত্রগুলি। আশা করা যায় এটি পড়লে আপনারা উপকৃত হতে পারবেন।
বহুল জিজ্ঞাসিত প্রশ্ন
১. আয়তক্ষেত্র কাকে বলে?
উত্তর: চতুর্ভুজ এর বিপরীত বাহুগুলো পরস্পর সমান হয় এবং প্রতিটি কোণ সমকোণ হয় তাকে আয়তক্ষেত্র বলে।
২. আয়তক্ষেত্রের বৈশিষ্ট্য গুলি কি কি?
উত্তর: বৈশিষ্ট্য গুলি হল-
- আয়তক্ষেত্রের চারটি শীর্ষবিন্দু এবং চারটি বাহু রয়েছে।
- প্রতিটি আয়তক্ষেত্রই একটি চতুর্ভুজ।
- আয়তক্ষেত্র একটি অনিয়মিত বহুভুজ।
- এর প্রতিটি কোণ ৯০ ডিগ্রী বা সমকোণ।
Also Read: রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র

