সমকোণী ত্রিভুজ কাকে বলে ! সমকোণী ত্রিভুজের বৈশিষ্ট্য 

জ্যামিতির অন্যতম গুরুপ্তপূর্ণ ধারণা হলো সমকোণী ত্রিভুজে সম্পর্কে জানা, সমকোণী ত্রিভুজ ভালোভাবে না বুঝলে পিথাগোরাস উপপাদ্য বোঝা সম্ভব না।  আজকের এই লেখায় আমরা জন্য সমকোণী ত্রিভুজ কাকে বলে ও এই সম্বন্ধীয় যাবতীয় বিষয় সম্পর্কে।  

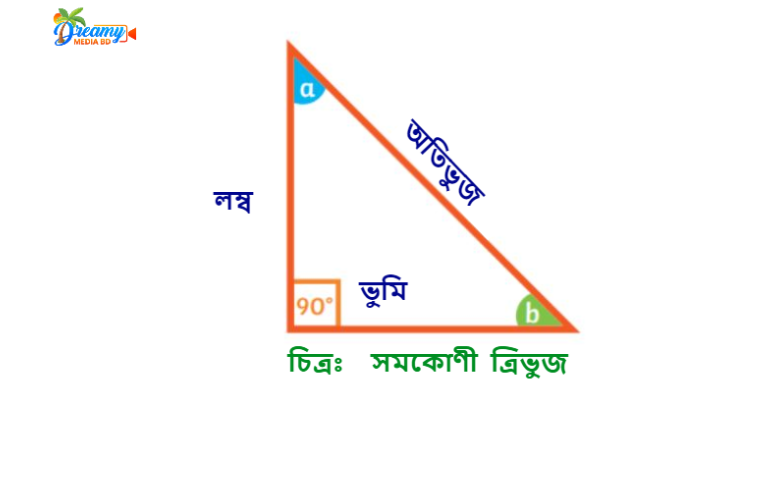
সমকোণী ত্রিভুজ কাকে বলে 

সমকোণী ত্রিভুজ হল এমন একটি ত্রিভুজের একটি কোণ সমকোণ বা ৯০ ডিগ্রি। 

অর্থাৎ, যে ত্রিভুজের একটি কোণ সমকোণ ৯০ ডিগ্রী এবং অন্য দুটি কোণের সমষ্টি এক সমকোণ বা ৯০ ডিগ্রি হলে তাকে সমকোণী ত্রিভুজ বলে।

সমকোণী ত্রিভুজের তিনটি সংজ্ঞা:

• প্রথম সংজ্ঞা: যে ত্রিভুজের একটি কোণ সমকোণ বা ৯০ ডিগ্রি, তাকে সমকোণী ত্রিভুজ বলে।
• দ্বিতীয় সংজ্ঞা: যে ত্রিভুজের তিনটি কোণের সমষ্টি ১৮০ ডিগ্রি, এবং এর মধ্যে একটি কোণ সমকোণ, তাকে সমকোণী ত্রিভুজ বলে।
• তৃতীয় সংজ্ঞা: যে ত্রিভুজের যেকোনো একটি বাহুর বর্গ অপর দুই বাহুর বর্গের সমষ্টির সমান, তাকে সমকোণী ত্রিভুজ বলে।

সমকোণী ত্রিভুজের বৈশিষ্ট্য 

• সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয়কে লম্ব এবং ভূমি বলে।
• সমকোণী ত্রিভুজের লম্ব এবং ভূমির বিপরীত বাহুকে  অতিভুজ বলে।
• সমকোণী ত্রিভুজের লম্ব, ভূমি এবং অতিভুজের মধ্যে একটি নির্দিষ্ট সম্পর্ক বিদ্যমান, যা পিথাগোরাসের উপপাদ্য দ্বারা প্রকাশ করা হয়।
• ত্রিভুজে তিনটি বাহু এবং তিনটি কোণ থাকে।
• সমকোণী ত্রিভুজের একটি কোণ ৯০ ডিগ্রি হবে।
• সমকোণী ত্রিভুজের অন্য দুটি কোণের যোগফল ৯০ ডিগ্রি হবে।
•  সমকোণী ত্রিভুজের তিনটি বাহুর মধ্যে একটি বাহু সবচেয়ে লম্বা হবে, যাকে অতিভুজ বলা হয়।
• অতিভুজের বিপরীত কোণটি সবচেয়ে বড় কোণটি হবে, যাকে সমকোণ বলা হয়।
• সমকোণী ত্রিভুজের অন্য দুটি বাহুকে আনুভুজ বলা হয়।
• সমকোণী ত্রিভুজের তিনটি বাহুর মধ্যে অতিভুজের বর্গ অন্য দুটি আনুভুজের বর্গের যোগফলের সমান হবে।
• সমকোণী ত্রিভুজের যে কোনো একটি সমকোণের বিপরীত আনুভুজটি অতিভুজের অর্ধেক হবে।
• সমকোণী ত্রিভুজের যে কোনো একটি সমকোণের বিপরীত আনুভুজটি অতিভুজের বর্গমূলের বর্গের চতুর্থাংশের সমান হবে।
• সমকোণী ত্রিভুজের যে কোনো একটি সমকোণের বিপরীত আনুভুজটি অতিভুজের সাইন (sine) ফাংশনের সমান হবে।
• সমকোণী ত্রিভুজের যে কোনো একটি সমকোণের বিপরীত আনুভুজটি অতিভুজের কোসাইন (cosine) ফাংশনের সমান হবে।
• সমকোণী ত্রিভুজের যে কোনো একটি সমকোণের বিপরীত আনুভুজটি অতিভুজের ট্যাংজেন্ট (tangent) ফাংশনের সমান হবে।

সমকোণী ত্রিভুজের ক্ষেত্রফল 

সমকোণী ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র:

সমকোণী ত্রিভুজের ক্ষেত্রফল = (১/২) × লম্ব × ভূমি

যেখানে,

• লম্ব = সমকোণী ত্রিভুজের লম্ব বাহুর দৈর্ঘ্য
• ভূমি = সমকোণী ত্রিভুজের ভূমি বাহুর দৈর্ঘ্য

উদাহরণস্বরূপ, ধরুন একটি সমকোণী ত্রিভুজের লম্ব বাহুর দৈর্ঘ্য ৫ সেমি এবং ভূমি বাহুর দৈর্ঘ্য ১০ সেমি। তাহলে, ত্রিভুজটির ক্ষেত্রফল হবে:

ক্ষেত্রফল = (১/২) × ৫ × ১০

= ২৫ বর্গ সেমি

সমকোণী ত্রিভুজের ক্ষেত্রফলের অন্যান্য সূত্র

• পিথাগোরাসের উপপাদ্য ব্যবহার করে:

ক্ষেত্রফল = (১/২) × অতিভুজ × লম্ব

• ভূমির অর্ধপরিসীমা ব্যবহার করে:

ক্ষেত্রফল = (১/২) × ভূমির অর্ধপরিসীমা × লম্ব

• ভূমির অর্ধপরিসীমা এবং অতিভুজের মধ্যে সম্পর্ক ব্যবহার করে:

ক্ষেত্রফল = (১/২) × ভূমির অর্ধপরিসীমা × অতিভুজ

সমকোণী ত্রিভুজের পরিসীমা 

সমকোণী ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র:

পরিসীমা = ২(লম্ব + ভূমি)

যেখানে,

• লম্ব = সমকোণী ত্রিভুজের লম্ব বাহুর দৈর্ঘ্য
• ভূমি = সমকোণী ত্রিভুজের ভূমি বাহুর দৈর্ঘ্য

উদাহরণস্বরূপ, ধরুন একটি সমকোণী ত্রিভুজের লম্ব বাহুর দৈর্ঘ্য ৫ সেমি এবং ভূমি বাহুর দৈর্ঘ্য ১০ সেমি। তাহলে, ত্রিভুজটির পরিসীমা হবে:

পরিসীমা = ২(৫ + ১০)

= ২৫ সেমি

সমকোণী ত্রিভুজের পরিসীমা নির্ণয়ের সমস্যা সমাধানের কৌশল

• প্রথমে ত্রিভুজের লম্ব এবং ভূমির দৈর্ঘ্য নির্ণয় করুন।
• লম্ব এবং ভূমি নির্ণয়ের পর, পরিসীমা নির্ণয়ের সূত্রটি ব্যবহার করে ত্রিভুজটির পরিসীমা নির্ণয় করুন।

সমকোণী ত্রিভুজের পরিসীমা নির্ণয়ের অন্যান্য সূত্র

• অতিভুজ ব্যবহার করে:

পরিসীমা = ২(অতিভুজ)

• ভূমির অর্ধপরিসীমা ব্যবহার করে:

পরিসীমা = ২(ভূমির অর্ধপরিসীমা)

• লম্ব এবং ভূমির অর্ধপরিসীমা ব্যবহার করে:

পরিসীমা = (লম্ব + ভূমি) + (লম্ব + ভূমি)

= ২(লম্ব + ভূমি)

পিথাগোরাসের উপপাদ্য 

পিথাগোরাসের উপপাদ্য হল জ্যামিতির একটি গুরুত্বপূর্ণ উপপাদ্য, যা সমকোণী ত্রিভুজের লম্ব, ভূমি এবং অতিভুজের মধ্যে সম্পর্ক প্রকাশ করে।

পিথাগোরাসের উপপাদ্য:

কোনো সমকোণী ত্রিভুজের লম্ব এবং ভূমির বর্গের সমষ্টি অতিভুজের বর্গের সমান।

সূত্র:

a^2 + b^2 = c^2

যেখানে,

• a = লম্ব
• b = ভূমি
• c = অতিভুজ

পিথাগোরাসের উপপাদ্যের প্রমাণ:

প্রমাণ:

ধরি, ΔABC একটি সমকোণী ত্রিভুজ, যেখানে C হল সমকোণ।

AB^2 + AC^2 = BC^2

[AB^2 + AC^2]/2 = [BC^2]/2

AB^2/2 + AC^2/2 = BC^2/2

(AB + AC)^2/2 = BC^2/2

(AB + AC)^2 = BC^2

পিথাগোরাসের উপপাদ্যের ব্যবহার

• সমকোণী ত্রিভুজের লম্ব, ভূমি এবং অতিভুজ নির্ণয় করতে।
• ত্রিকোণমিতির বিভিন্ন সূত্র প্রমাণ করতে।
• জ্যামিতিক সমস্যা সমাধান করতে।

কোন ত্রিভুজের সম্পাদ্য উপপাদ্য

কোন ত্রিভুজের তিনটি কোণের পরিমাপের যোগফল 180° হয়।

এই উপপাদ্যটি ত্রিভুজের কোণ সম্পর্কিত একটি মৌলিক উপপাদ্য। এটি ত্রিভুজের কোণ সংক্রান্ত অন্যান্য উপপাদ্য প্রমাণ করতে ব্যবহৃত হয়।

উপপাদ্যটির প্রমাণ:

ধরুন ABC ত্রিভুজের কোণগুলি হল A, B, এবং C। তাহলে,

A + B + C = ?

A কোণের বিপরীত বাহুর নাম AB, B কোণের বিপরীত বাহুর নাম BC, এবং C কোণের বিপরীত বাহুর নাম CA।

একটি ত্রিভুজের বাহুর বিপরীত কোণটি সেই বাহুর অন্তর্ভুক্ত কোণ।

সুতরাং,

AB + BC + CA = 180°

এটি প্রমাণিত যে, কোন ত্রিভুজের তিনটি কোণের পরিমাপের যোগফল 180° হয়।

উপপাদ্যটির ব্যবহার:

এই উপপাদ্যটি ত্রিভুজের কোণ সংক্রান্ত অন্যান্য উপপাদ্য প্রমাণ করতে ব্যবহৃত হয়। যেমন,

• কোনো ত্রিভুজের যেকোনো দুটি কোণের পরিমাপের যোগফল তৃতীয় কোণের পরিমাপের চেয়ে কম বা সমান হয়।
• কোনো ত্রিভুজের যেকোনো কোণের পরিমাপের যোগফল 90° হলে, ত্রিভুজটি সমকোণী হয়।

সমকোণী ত্রিভুজের গুরুত্ব

• সমকোণী ত্রিভুজ বিভিন্ন জ্যামিতিক সমস্যা সমাধানে ব্যবহৃত হয়। যেমন, একটি ত্রিভুজের ক্ষেত্রফল নির্ণয়, একটি দূরত্ব নির্ণয়, একটি কোণ পরিমাপ ইত্যাদি।
• সমকোণী ত্রিভুজ ত্রিকোণমিতির একটি গুরুত্বপূর্ণ বিষয়। ত্রিকোণমিতি হল জ্যামিতির একটি শাখা যা ত্রিভুজ এবং ত্রিকোণীয় ফাংশনগুলির সাথে সম্পর্কিত।
• সমকোণী ত্রিভুজ বিভিন্ন ক্ষেত্রের প্রকৌশল কাজে ব্যবহৃত হয়। যেমন, নির্মাণ, স্থাপত্য, ইলেকট্রনিক্স, মেকানিক্যাল ইঞ্জিনিয়ারিং ইত্যাদি।

সমকোণী ত্রিভুজ সম্পর্কিত প্রশ্নাবলী – FAQ 

সমকোণী ত্রিভুজের প্রতিটি কোণের মান কত?

সমকোণী ত্রিভুজের একটি কোণ সমকোণ বা ৯০ ডিগ্রি। অন্য দুটি কোণের সমষ্টি এক সমকোণ বা ৯০ ডিগ্রি। 

সমকোণী ত্রিভুজের বাহুগুলোর অনুপাত কত?

সমকোণী ত্রিভুজের বাহুগুলোর অনুপাত সাধারণত ১:১:√২। এই অনুপাতটি পিথাগোরাসের উপপাদ্যের উপর ভিত্তি করে গঠিত।

সমকোণী ত্রিভুজের বাহুর যোগফল কত?

সমকোণী ত্রিভুজের বাহুর যোগফল পরিসীমার সমান। পরিসীমা হল ত্রিভুজটির তিনটি বাহুর দৈর্ঘ্যের যোগফল। সুতরাং, সমকোণী ত্রিভুজের বাহুর যোগফল হবে:

বাহুর যোগফল = পরিসীমা

বাহুর যোগফল = ২(লম্ব + ভূমি)

কোন ত্রিভুজের দুইটি কোণ ছাড়া তৃতীয় বাহুর নির্ণয় কি সম্ভব? 

কোন ত্রিভুজের দুইটি কোণ ছাড়া তৃতীয় বাহুর নির্ণয় করা সম্ভব। তবে, এক্ষেত্রে ত্রিভুজটির পরিসীমা বা ত্রিভুজটির একটি বাহুর দৈর্ঘ্য এবং অপর দুইটি বাহুর অন্তর্ভুক্ত কোণের মান জানা থাকতে হবে।

ত্রিভুজের সন্নিহিত বাহু কোনটি?

ত্রিভুজের যেকোনো দুটি কোণের অন্তর্ভুক্ত বাহুকে সন্নিহিত বাহু বলে। অর্থাৎ, যেকোনো দুটি কোণ একই বাহুর দুই প্রান্তে মিলিত হলে সেই বাহুটি সন্নিহিত বাহু।

শেষ কথা 

প্রিয় শিক্ষার্থী বন্ধুরা আজকের এই লেখায় আমরা জানলাম সমকোণী ত্রিভুজ কাকে বলে ও এই সম্বন্ধীয় যাবতিয় প্রয়োজনীয় বিষয়ের এর বিস্তারিত আলোচনা।  আমাদের এই ব্লগে আমরা নিয়মিত এই জাতীয় লেখা প্ৰকাশ করি।  তাই, আমাদের ব্লগটি নিয়মিত পড়ুন।  ধন্যবাদ।  

Also Read:  ত্রিভুজ কাকে বলে?