রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র 

যে চতুর্ভুজ এর চারটি বাহু পরস্পর সমান্তরাল ও সমান হয় কিন্তু কোনগুলি সমকোণ নয় টাকি রম্বস বলা হয়। আজকের এই আর্টিকেলে আমরা রম্ব সম্পর্কে আলোচনা করব রম্বস কাকে বলে, রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র, রম্বসের ক্ষেত্র দৈর্ঘ্য নির্ণয়ের সূত্র, পরিসীমা নির্ণয়ের সূত্র, কর্ণ নির্ণয়ের সূত্র ইত্যাদি।

রম্বস কাকে বলে

একটি সামান্তরিক এর দুইটি সন্নিহিত বাহু সমান হয়ে থাকলে তাকে রম্বস বলা হয়। 

অন্যভাবে বলা যায় যে চারটি বাহু দ্বারা একটি ক্ষেত্র সীমাবদ্ধ এবং যার  কোণ ও সমকোণ একটি নয় তাকেই রম্বস বলা হয়। রম্বসের বৈশিষ্ট্য গুলি হল –

• রম্বসের চারটি বাহু সমান হয়ে থাকে। 
• রম্বসের কোণগুলি সমকোণ নয়। 
• রম্বসের সন্নিহিত কোণগুলির সমষ্টি দুই সমকোণ। 
• রম্বসের কর্ণগুলি সমকোণে সমদ্বিখন্ডিত করে থাকে। 
• রম্বসের বিপরীত কোণদ্বয় পরস্পর সমান হয়ে থাকে।

রম্বস সম্পর্কিত সূত্র সমূহ

রম্বসের পরিসীমা নির্ণয়ের সূত্র 

রম্বসের বাহুগুলির সমষ্টিকে বলা হয় রম্বসের পরিসীমা। রম্বসের দুইটি কর্ণ সম্পর্কে জানা থাকলে রম্বসের বাহুর দৈর্ঘ্যও নির্ণয় করা যায় এবং রম্বসের পরিসীমা নির্ণয় করা সম্ভব।

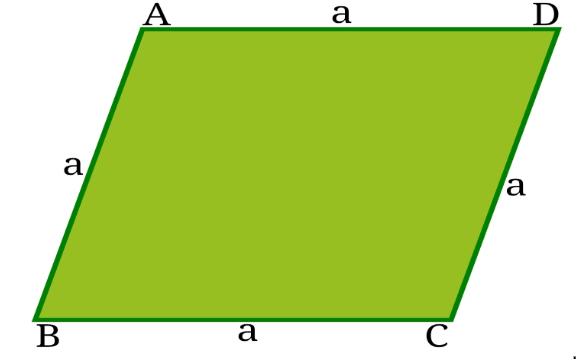
মনে করি, ABCD একটি রম্বস এবং AB = BC = CD = AD = a.

আমরা জানি, রম্বসের বাহুগুলো পরস্পর সমান।

সুতরাং, রম্বসের পরিসীমা P হলে,

P = (AB + BC + CD + AD) একক

বা, P = (a + a + a + a) একক

∴ P = 4a একক

রম্বসের বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র 

রম্বসের কর্ণ গুলি জানা থাকলেই রম্বসের বাহুর দৈর্ঘ্য নির্ণয় করা যায়। যেভাবে রম্বসের বাহুর দৈর্ঘ্য নির্ণয় করা যাবে –

∴ AB2 + BC2 + CD2 + AD2 = d12 + d22

বা, a2 + a2 + a2 + a2 = d12 + d22

বা, 4a2 = d12 + d22

বা, a = √d12 + d22√4

∴ a = √d12 + d222

রম্বসের কর্ণ নির্ণয়ের সূত্র

রম্বসের বিপরীতে যে কৌণিক দুইটি বিন্দু রয়েছে সেগুলো যোগ করে যে রেখাংশ পাওয়া যায় তাকে বলা হয় রম্বসের কর্ণ। রম্বসের কর্ণ গুলি পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে থাকে।

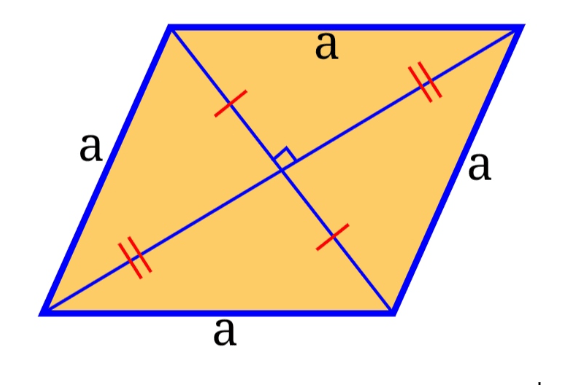
মনে করি, ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য AB, BC, CD ও AD; এবং AC ও BD এর দুইটি কর্ণ।

যেহেতু রম্বসের বাহুগুলো পরস্পর সমান, তাহলে মনে করি, AB = BC = CD = AD = a এবং কর্ণ AC = d1 ও BD = d2

△ABC -এ কোসাইন ল (law of cosines) হতে পাই,

AC2 = AB2 + BC2 – 2AB.BC.cosB

বা, d12 = a2 + a2 – 2a.a cosB

বা, d1 = √2a2 – 2a2 cosB

বা, d1 = √2a2 – 2a2 cos(180°-A) [∵ A + B = 180°]

বা, d1 = √2a2 – 2a2 (-cosA)

বা, d1 = √2a2 + 2a2 cosA

বা, d1 = √a2(2 + 2cosA)

∴ d1 = a√2 + 2cosA

আবার, △ABD -এ কোসাইন ল (law of cosines) হতে পাই,

BD2 = AB2 + AD2 – 2AB.AD.cosA

বা, BD = √AB2 + AD2 – 2AB.AD.cosA

বা, d2 = √AB2 + AD2 – 2a.a cosA

বা, d2 = √a2 + a2 – 2a2cosA

বা, d2 = √2a2 – 2a2cosA

বা, d2 = √a2(2 – 2cosA)

বা, d2 = a√2 – 2cosA

রম্বসের উচ্চতা নির্ণয়ের সূত্র

একটি রম্বসের উচ্চতা পেতে হলে এই সূত্রটি ব্যবহার করতে হবে  উচ্চতা = ক্ষেত্রফল ÷ ভিত্তি । যদি আপনি একটি রম্বসের কর্ণ জেনে থাকেন  কিন্তু  ক্ষেত্রফল না জানেন , তাহলে এই সূত্র ব্যবহার করতে হবে  = (d1 x d2) ÷ 2 , এরপর  প্রথম সূত্রে ক্ষেত্রফল প্রয়োগ করতে হবে। 

রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্রের প্রমাণ বা ব্যাখ্যা 

রম্বসের একটি বাহু ও সন্নিহিত কোণ এর পরিমাপের মাধ্যমে কর্ণ নির্ণয় করা সম্ভব এবং কর্ণদ্বয়ের মান ব্যবহারের মাধ্যমে রম্বসের ক্ষেত্রফল নির্ণয় করা যায়।

প্রথম পদ্ধতি: রম্বসের কর্ণদ্বয়ের গুণফলকে অর্ধেক করলে ক্ষেত্রফল পাওয়া যায়। 

অতএব, রম্বসের ক্ষেত্রফল নির্ণয়ের সুত্র 1/2 × কর্ণদ্বয়ের গুণফল 

ABCD রম্বসের কর্ণ দুইটি d1 ও d2 হলে, এর ক্ষেত্রফল হবে

A = 12 d1d2 বর্গ একক

দ্বিতীয় পদ্ধতি: রম্বসের যেকোনো কোণ এর সাইনকে বাহুর বর্গ দিয়ে গুন করলেই রম্বসের ক্ষেত্রফল পাওয়া যাবে।

মনে করি, ABCD রম্বসের বাহু a এবং ক্ষেত্রফল A হলে,

A = a2sinA বর্গ একক

চতুর্থ পদ্ধতিঃ মনে করি, ABCD রম্বসের বাহুর দৈর্ঘ্য a এবং BD একটি কর্ণ।

□ABCD = △ABD + △BCD

বা, □ABCD = △ABD + △ABD [∵ △ABD ≅ △BCD]

বা, □ABCD = 2△ABD

বা, □ABCD = 2. 12 a. a sinA

∴ □ABCD = a2sinA

বিসিএস এবং অন্যান্য চাকরীর আবেদন পরীক্ষায় আসা কিছু প্রশ্নের উত্তর।

১. কোন  সামান্তরিকের চারটি বাহু পরস্পর সমান, কিন্তু কর্ণদ্বয় পরস্পর অসমান। তাকে কি বলে? ( প্র. শি. স. চা.) 

উত্তর: রম্বস। 

২. একটি রম্বস আঁকতে হলে কমপক্ষে কোন উপাত্ত গুলোর প্রয়োজন? ( প্র. শি. স. চা.) 

উত্তর: এক বাহু ও এক কোণ। 

৩. রম্বসের কর্ণদ্বয় পরস্পর O বিন্দুতে ছেদ করেছে, কর্ণদ্বয়ের অন্তর্ভুক্ত কোণ-( প্র. শি. স. চা.) 

উত্তর: সমকোণ। 

৪. যে সামান্তরিকের সকল বাহু সমান কিন্তু কোণ গুলো সমান নয়, তাকে বলে- ( প্র. শি) 

উত্তর: রম্বস। 

৫. চারটি সমান বাহু দ্বারা সীমাবদ্ধ একটি ক্ষেত্র যার একটি কোণও সমকোণ নয়, এরূপ চিত্রকে বলা হয়- ( বিসিএস, স.চা.)

উত্তর: রম্বস। 

শেষকথা

রম্বস এমন ধরনের সামান্তরিক যার বাহুবলি পরস্পর সমান হয়ে থাকে। রম্বস কে অনেক সময় বলা হয় হীরা কারণ একে দেখতে অনেকটা হীরার মত মনে হয়। রম্বসের কর্ণ গুলি কোন গুলিকে সমদিখন্ডিত করে থাকে এবং সবগুলি বাহুর দৈর্ঘ্য পরস্পর সমান হওয়ার জন্য একে সমবাহু চতুর্ভুজও বলা হয়ে থাকে। আশা করি এই  আর্টিকেল পড়লে আপনি রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্রসহ অন্যান্য বিষয় সম্পর্কে জানতে পারবেন।

Also Read: ত্রিকোণমিতির সকল সূত্রসমূহ