ত্রিভুজ কাকে বলে? 

ত্রিভুজ কাকে বলে? বা ত্রিভুজের ধারণা গণিতের একটি গুরুপ্তপূর্ণ বিষয়।  ত্রিভুজের ক্লিয়ার ধারণা ছাড়া গণিত ভালোভাবে বোঝো সম্ভব নয়।  আজকের এই লেখায় আমরা ত্রিভুজের সংজ্ঞা,ধারণা, প্রকারভেদ সহ ইত্যাদি গুরুপ্তপূর্ণ বিষয় নিয়ে আলোচনা করবো।  

 

ত্রিভুজ কাকে বলে? 

ত্রিভুজ হল একটি দ্বিমাত্রিক বহুভুজ যার তিনটি কোণ এবং তিনটি বাহু আছে। 

ত্রিভুজের সংজ্ঞা:

• ত্রিভুজ হল তিনটি বাহু এবং তিনটি কোণ বিশিষ্ট একটি বহুভুজ।
• ত্রিভুজ হল এমন একটি বহুভুজ যার তিনটি বাহু এবং তিনটি শীর্ষবিন্দু রয়েছে।
• ত্রিভুজ হল এমন একটি বহুভুজ যার তিনটি কোণের সমষ্টি সর্বদা ১৮০ ডিগ্রি।
• ত্রিভুজ হল এমন একটি বহুভুজ যার তিনটি বাহু একটি সমতলে অবস্থিত।

ত্রিভুজের পরিচয় 

ত্রিভুজের বিভিন্ন অংশের পরিচয় নিম্নরূপ:

• শীর্ষবিন্দু: ত্রিভুজের তিনটি বিন্দুকে শীর্ষবিন্দু বলে।
• বাহু: ত্রিভুজের তিনটি সরলরেখাংশকে বাহু বলে।
• কোণ: ত্রিভুজের দুটি বাহুর মধ্যবর্তী স্থান।

• ভূমি: ত্রিভুজের যেকোনো একটি বাহুর দৈর্ঘ্যকে ভূমি বলে।
• উচ্চতা: ভূমির উপর লম্বভাবে ত্রিভুজের ভিতরে আঁকা একটি রেখাকে উচ্চতা বলে।
• পরিধি: ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের যোগফলকে পরিধি বলে।
• অন্তঃকেন্দ্র: ত্রিভুজের অভ্যন্তরে অবস্থিত এমন একটি বিন্দু যেখান দিয়ে ত্রিভুজের তিনটি মধ্যমাও যায় তাকে অন্তঃকেন্দ্র বলে।
• পরিকেন্দ্র: ত্রিভুজের তিনটি বাহুর মধ্যবিন্দুগুলিকে যোগ করে যে ত্রিভুজটি গঠিত হয় তার শীর্ষবিন্দুগুলিকে পরিকেন্দ্র বলে।
• গৌণ বৃত্ত: ত্রিভুজের তিনটি শীর্ষবিন্দুকে কেন্দ্র করে আঁকা বৃত্তকে গৌণ বৃত্ত বলে।
• অভ্যন্তরীণ বৃত্ত: ত্রিভুজের তিনটি অন্তঃকেন্দ্রকে কেন্দ্র করে আঁকা বৃত্তকে অভ্যন্তরীণ বৃত্ত বলে।

ত্রিভুজের প্রকারভেদ সমূহ

ত্রিভুজের কোণগুলোর মান অনুসারে এবং বাহুর দৈর্ঘ্যের অনুপাত অনুসারে বিভিন্ন শ্রেণিতে ভাগ করা হয়ঃ 

কোণ অনুসারে ত্রিভুজ

• সূক্ষ্মকোণী ত্রিভুজ (Acute angle triangle): একটি ত্রিভুজকে সূক্ষ্মকোণী ত্রিভুজ বলা হয় যদি এর সমস্ত কোণ ৯০ ডিগ্রির চেয়ে কম হয়।
• সমকোণী ত্রিভুজ (Right angle triangle): একটি ত্রিভুজকে সমকোণী ত্রিভুজ বলা হয় যদি এর একটি কোণ ৯০ ডিগ্রি হয়।
• স্থুলকোণী ত্রিভুজ (Obtuse angle triangle): একটি ত্রিভুজকে স্থুলকোণী ত্রিভুজ বলা হয় যদি এর একটি কোণ ৯০ ডিগ্রির চেয়ে বেশি হয়।

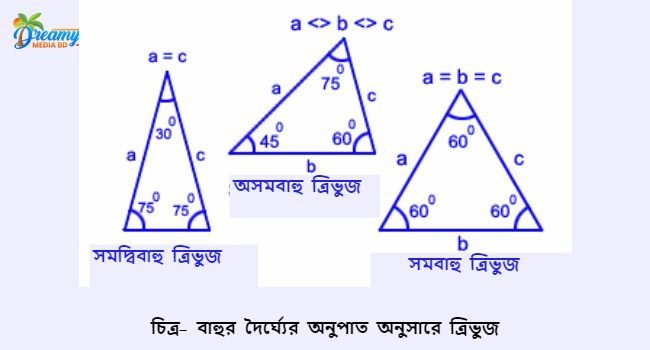
বাহুর দৈর্ঘ্যের অনুপাত অনুসারে ত্রিভুজ

• সমবাহু ত্রিভুজ (Equilateral triangle): একটি ত্রিভুজকে সমবাহু ত্রিভুজ বলা হয় যদি এর সমস্ত বাহু সমান হয়।
• সমদ্বিবাহু ত্রিভুজ (Isosceles triangle): একটি ত্রিভুজকে সমদ্বিবাহু ত্রিভুজ বলা হয় যদি এর দুটি বাহু সমান হয়।
• অসমবাহু ত্রিভুজ (Scalene triangle): একটি ত্রিভুজকে অসমবাহু ত্রিভুজ বলা হয় যদি এর কোনও দুটি বাহু সমান না হয়।

অন্যান্য শ্রেণীবিভাগ

• অন্তর্গামী ত্রিভুজ (Inscribed triangle): একটি ত্রিভুজকে অন্তর্গামী ত্রিভুজ বলা হয় যদি এটি একটি বৃত্তের ভিতরে অবস্থিত হয়।
• বহির্গত ত্রিভুজ (Exscribed triangle): একটি ত্রিভুজকে বহির্গত ত্রিভুজ বলা হয় যদি এটি একটি বৃত্তের বাইরে অবস্থিত হয়।
• প্রত্যান্ত ত্রিভুজ (Exterior triangle): একটি ত্রিভুজকে প্রত্যান্ত ত্রিভুজ বলা হয় যদি এটি একটি বৃত্তের বাইরে অবস্থিত হয় এবং এর তিনটি শীর্ষবিন্দু বৃত্তের উপর অবস্থিত হয়।

ত্রিভুজের সুত্র সমূহ

ক্ষেত্রফল নির্ণয়ের সূত্র

• ভূমি ও উচ্চতা দিয়ে নির্ণয়:

ক্ষেত্রফল = (ভূমি * উচ্চতা) / 2

 

• তিনটি বাহুর দৈর্ঘ্য দিয়ে নির্ণয়:

ক্ষেত্রফল = √(s(s-a)(s-b)(s-c)); এখানে s=(a+b+c)/2

কোণ সম্পর্কিত সূত্র

• ত্রিভুজের তিনটি কোণের সমষ্টি ১৮০°।
• কোনো ত্রিভুজের একটি কোণ ৯০° হলে, সেটিকে সমকোণী ত্রিভুজ বলে।
• সমকোণী ত্রিভুজের অতিভুজের বর্গ = ভূমি * লম্ব
• সমবাহু ত্রিভুজের তিনটি কোণ ৬০° এবং প্রতিটি বাহুর দৈর্ঘ্য সমান।
• সমদ্বিবাহু ত্রিভুজের দুটি সমান বাহুর বিপরীত কোণ সমান।

বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র

• কোনো ত্রিভুজের একটি কোণের বিপরীত বাহুর দৈর্ঘ্য = ত্রিভুজের ক্ষেত্রফল / (অন্য দুই বাহুর যোগফল) * (অন্য দুই বাহুর যোগফল – বিপরীত বাহুর দৈর্ঘ্য)
• কোনো ত্রিভুজের একটি বাহুর দৈর্ঘ্য = (অন্য দুই বাহুর দৈর্ঘ্য² – বিপরীত কোণের বিপরীত বাহুর দৈর্ঘ্য²)^(1/2)
• কোনো ত্রিভুজের একটি বাহুর দৈর্ঘ্য = (অন্য দুই বাহুর দৈর্ঘ্য * ত্রিভুজের ক্ষেত্রফল) / (অন্য দুই বাহুর বিপরীত কোণের যোগফল)

ত্রিভুজের পরিধি নির্ণয়ের সূত্র

• ত্রিভুজের পরিধি = তিনটি বাহুর যোগফল

ত্রিভুজের কর্ণ নির্ণয়ের সূত্র

• ত্রিভুজের কর্ণের দৈর্ঘ্য = (ত্রিভুজের ক্ষেত্রফল * 2) / (ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের যোগফল)

ত্রিভুজের পরিকেন্দ্র নির্ণয়ের সূত্র

• ত্রিভুজের পরিকেন্দ্রের দৈর্ঘ্য = (2 * ত্রিভুজের ক্ষেত্রফল) / (ত্রিভুজের তিনটি বাহুর যোগফল)

ত্রিভুজের অন্তঃকেন্দ্র নির্ণয়ের সূত্র

• ত্রিভুজের অন্তঃকেন্দ্রের দৈর্ঘ্য = (3 * ত্রিভুজের ক্ষেত্রফল) / (ত্রিভুজের তিনটি বাহুর মধ্যমাগুলির যোগফল)

ত্রিভুজের ভরকেন্দ্র নির্ণয়ের সূত্র

• ত্রিভুজের ভরকেন্দ্রের অবস্থান = (ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের গুণফলের যোগফল) / (ত্রিভুজের ক্ষেত্রফল * 3)

গনিতে ত্রিভুজের গুরুত্ব

ত্রিভুজ হল জ্যামিতির একটি মৌলিক গঠন বা আকৃতি যা গনিতে বিভিন্ন উপায়ে ব্যবহৃত হয়। ত্রিভুজের গুরুত্ব গনিতে নিম্নরূপ:

• ত্রিকোণমিতি হল জ্যামিতি এবং বীজগণিতের একটি শাখা যা ত্রিভুজের  সাথে সম্পর্কিত। ত্রিকোণমিতি বিভিন্ন ক্ষেত্রে ব্যবহৃত হয়, যেমন প্রকৌশল, ভূগোল, এবং জ্যোতির্বিজ্ঞান।
• ত্রিভুজ কাঠামোগত নকশায় অত্যন্ত শক্তিশালী এবং টেকসই ভুমিকা পালন করে। 

ত্রিভুজের বিজ্ঞানে ব্যবহারের কিছু উদাহরণ:

• ব্রিজ নির্মাণে, ত্রিভুজের ধারনার ব্যাপক ব্যাবহার করা হয়। উদাহরণস্বরূপ, একটি ত্রিভুজাকার টাওয়ার একটি বর্গাকার বা আয়তাকার টাওয়ারের চেয়ে বেশি স্থিতিশীল।
• জ্যোতির্বিজ্ঞানে, ত্রিকোণমিতি ব্যবহার করে আমরা সূর্য, চাঁদ এবং গ্রহগুলির অবস্থান নির্ধারণ করতে পারি।
• ভূগোলবিদরা ত্রিকোণমিতি ব্যবহার করে ভূপৃষ্ঠের দূরত্ব এবং উচ্চতা পরিমাপ করতে পারেন।
• ভূমি জরিপকারীরা ত্রিকোণমিতি ব্যবহার করে জমির সীমানা নির্ধারণ করতে পারেন।

ত্রিভুজ বিজ্ঞানের বিভিন্ন শাখায় একটি গুরুত্বপূর্ণ ভূমিকা পালন করে। তারা আমাদের চারপাশের বিশ্বকে বুঝতে আমাদের সাহায্য করে।

ধারাবাহিক প্রশ্ন উত্তর 

সমবাহু ত্রিভুজের অপর নাম কী?

 

সমবাহু ত্রিভুজের অপর নাম হল “ইকুইল্যাটেরাল ত্রিভুজ”। এই ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য একই হয়ে থাকে।

ত্রিভুজ সম্পর্কিত উপপাদ্য সমূহ কি? 

 

ত্রিভুজ সম্পর্কিত বিভিন্ন উপপাদ্য রয়েছে। এর মধ্যে কিছু গুরুত্বপূর্ণ উপপাদ্য হল:

ত্রিভুজের কোণগুলোর সমষ্টি উপপাদ্য:

একটি ত্রিভুজের তিনটি কোণের সমষ্টি সর্বদা ১৮০ ডিগ্রি হয়।

ত্রিভুজের বাহুর অনুপাত উপপাদ্য:

একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের অনুপাত তাদের বিপরীত কোণের অনুপাতের সমান।

ত্রিভুজের বাহুর ক্ষেত্রফল উপপাদ্য:

একটি ত্রিভুজের ক্ষেত্রফল তার ভূমির অর্ধেক ও উচ্চতার গুণফলের সমান।

ত্রিকোণমিতি সম্পর্কিত উপপাদ্য:

• সমকোণী ত্রিভুজের:
  • পিথাগোরাসের উপপাদ্য: একটি সমকোণী ত্রিভুজের অতিভুজের বর্গ তার অন্যান্য দুইটি বাহুর বর্গের সমষ্টির সমান।
  • হিপোমেনস থেকে লম্বের দূরত্ব: একটি সমকোণী ত্রিভুজের হিপোমেনস থেকে লম্বের দূরত্ব হিপোমেনস ও লম্বের অনুপাত বর্গমূলের সমান।
• সমান্তরাল সরলরেখা:
  • দুটি সমান্তরাল সরলরেখার মধ্যে অবস্থিত একটি ত্রিভুজের বিপরীত কোণগুলি পরস্পর সমান।
  • দুটি সমান্তরাল সরলরেখার মধ্যে অবস্থিত একটি ত্রিভুজের বিপরীত বাহুগুলি পরস্পর সমান্তরাল।

 

একটি ত্রিভুজের তিনটি বাহু দ্বারা আবদ্ধ ক্ষেত্রকে কি বলে?

একটি ত্রিভুজের তিনটি বাহু দ্বারা আবদ্ধ ক্ষেত্রকে ত্রিভুজের ক্ষেত্রফল বলে। ত্রিভুজের ক্ষেত্রফল নির্ণয়ের জন্য বিভিন্ন সূত্র রয়েছে। এর মধ্যে একটি সূত্র হল:

ত্রিভুজের ক্ষেত্রফল = (ভূমি * উচ্চতা) / 2

 

যেখানে,

• ভূমি হল ত্রিভুজের যেকোনো একটি বাহুর দৈর্ঘ্য।
• উচ্চতা হল ভূমির উপর লম্বভাবে ত্রিভুজের ভিতরে আঁকা একটি রেখা।

অতিভুজ কাকে বলে? 

অতিভুজ হল একটি সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহু। অতিভুজ ত্রিভুজের বৃহত্তম বাহু। এটির বর্গ অন্য দুটি বাহুর বর্গের সমষ্টির সমান, যেটি পিথাগোরাসের উপপাদ্য নামে পরিচিত।

Also read: সন্নিহিত কোণ কাকে বলে?